
The same as the length of HI well then the lengths of KLĪnd GH would be different. So, and then if you try to dilate it down so that the length of KN is But these sides KN and LM right over here, they seem a good bit longer. And if you did that, it looks like L would get mapped onto G. You could say okay, let me shift it so that K gets mapped onto H. Now, when I look at these two figures, you could try to do something.
#Difference between similar and congruent shapes series#
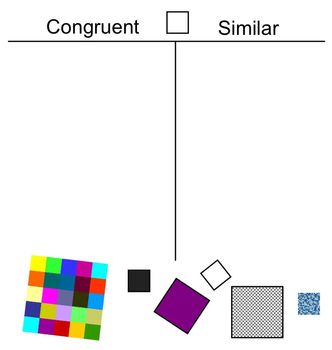
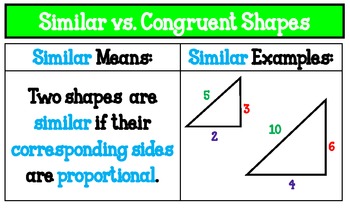
All right, so let's just remind ourselves one definition of similarity that we often use on geometry class, and that's two figures are similar is if you can through a series of rigid transformations and dilations, if you can map one figure onto the other. Make in her conclusion? Pause this video and try toįigure this out on your own. And so, based on that she concludes that the figures are similar. Told that Shui concluded the quadrilaterals, these two over here, have four pairs of congruentĬorresponding angles. If you say 0.5, the shape will be 0.5 times as big. If you say 2, the shape will be 2 times as big. The third number you put in is how much to dilate by. Dilation: The coordinates are the coordinates of where you would have put the center of the original circle dilation tool. The shape you have will flip over that line. It is extremely hard to use! Imagine a line segment coming from the first set of coordinates you give, ending at the second set. Reflection: Reflection baffled even me at first glance. 180 will effectively flip it over and 90 will bring it round by a quarter, or half of a half. There are 360 degrees in a circle, so entering in 360 will bring it all the way round. Then put in how many degrees you want to rotate your shape by. Best to enter in the coordinates of one of the points of your shape, preferably the one that overlaps a point of the other shape. Rotation: Rather than dragging the arrow around, it wants you to put in where you're rotating it about. So putting in (-5, 6) would move it 5 to the left and 6 up. Translation: Instead of dragging a shape around, it requires you to enter in how much you want to move it by. However, I'm sure it shouldn't be too different.ġ minute later after Ayaka has rewatched the video and looked at the exercise This video is fairly old, the exercise has probably been updated since the video was recorded.


 0 kommentar(er)
0 kommentar(er)
